アメリカの小学校で習う掛け算のやり方は、日本と少し違っていて戸惑う親御さんもいるかと思います。2桁以上の掛け算の場合、日本なら「筆算」を書いて計算する方法が一般的ですが、アメリカでは数通りの計算方法を習います。
スタンダードアルゴリズム
まず日本でもなじみの深い ↓ このような計算は、Standard Algorithm (標準的な計算法)と呼ばれています。仰々しい名前ですが、筆算ですね。

ところで、繰り上げの数字、どこに書きますか?日本で習った私は上記のように足し忘れないように下に書きますが、アメリカの場合、425の数字の上に書いたりします。日本でもそう変わってきたのか、それともアメリカだけ?とよく疑問に思うのですが、アメリカの学校に通う生徒さんは、たいてい425の数字の上に書きます。でも、2桁×2桁になると、繰り上げの数字が入り乱れることになるので、個人的には下に書くの方分かりやすいかな、と思うのですが、みなさんどちらですか?
パーシャルプロダクトメソッド
次に、アメリカの小学校で習うのが、Partial Products Method (パーシャルプロダクトメソッド)と呼ばれる手法です。Partialとは「部分的」、Productとは「掛け算の積(答え)」の意味です。この方法は下の画像を見ていただくと分かりやすいかと思いますが、
425×6という計算で、425を400と20と5で成り立っていると考え、それぞれの数字に6をかけ、足し合わせる方法です。

通常の筆算でも同じ工程をだどっているのですが、繰り上げの間違いや桁を書く位置を間違えたりするミスが起こりにくくなります。なぜこういう計算になるのか、計算の意味も分かりやすいと思います。
エリアモデル
こちらはArea(面積)の考えを活用した計算方法です。
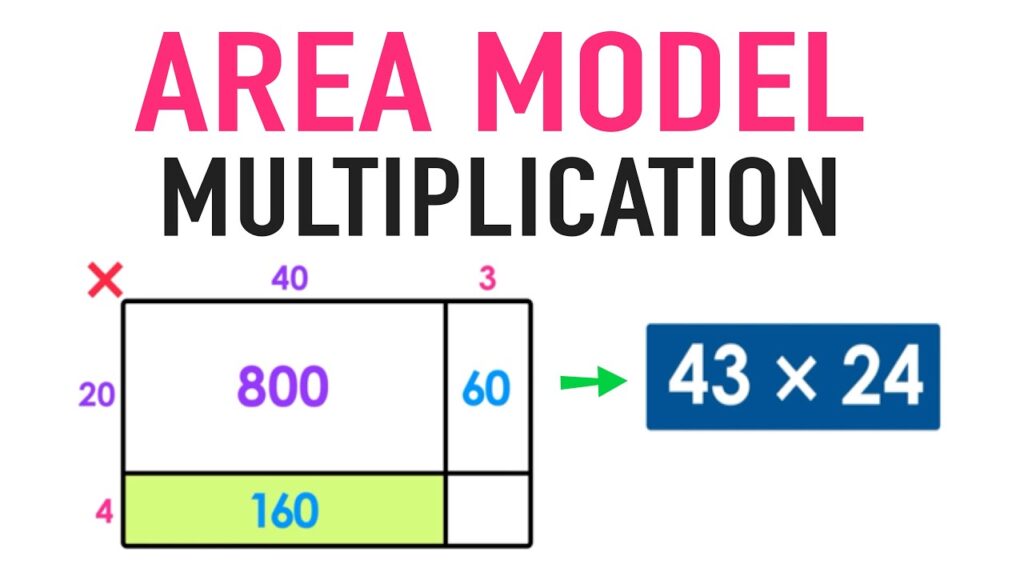
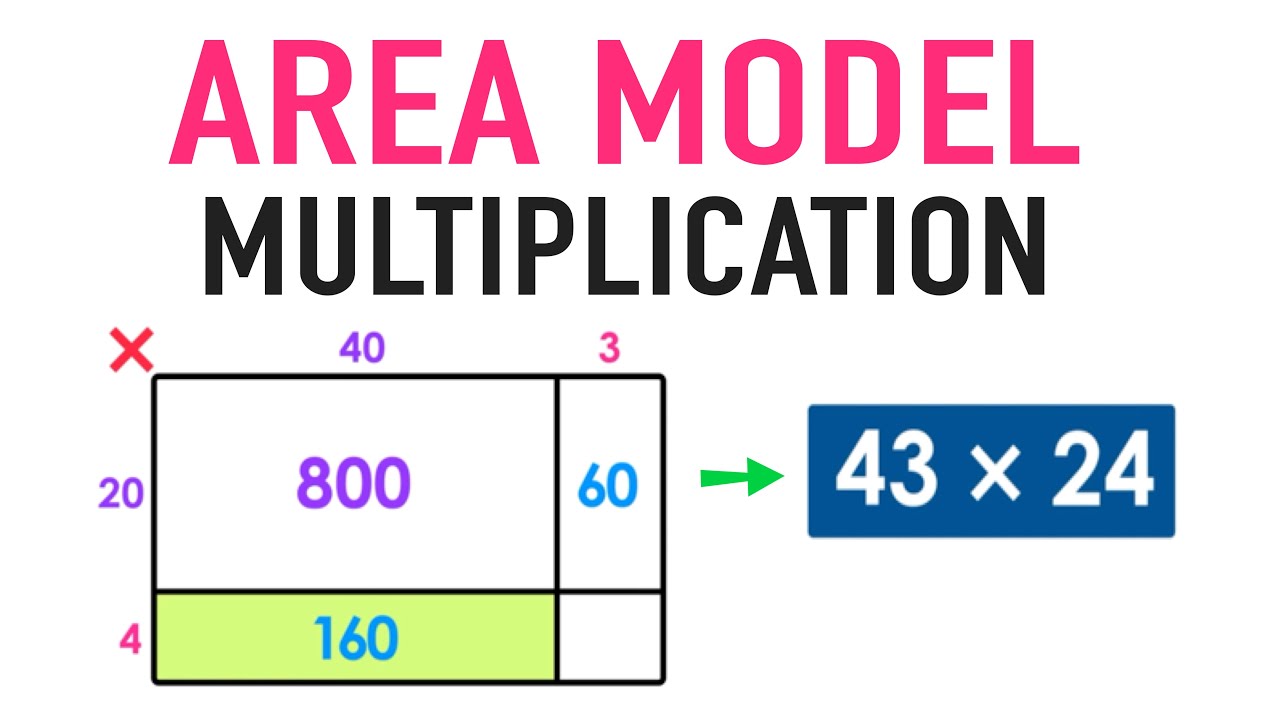
43×24という計算において、Partial Products Method と同様に43=40+3 に分け、24=20+4に分けて、それぞれを長方形の縦と横と考えます。そして各長方形の面積を足し上げるという方法です。
考えの根本は同じですが、視覚的に分かりやすいという利点があります。
日本式の筆算のやり方だけを学ぶよりも、数字を分解する練習、視覚化する練習、という意味で有益だと思います。こうした学習は特にEureka Mathと呼ばれるニューヨークの学校のカリキュラムに取り入れられています。
お子さんが宿題でこういう問題を持って帰ってきた場合は、ぜひ参考にしてみてください。